2019-11-08 Excel 2019
Egy szám rangsor-pozícióját százalékos értékkel is kifejezhetjük. Akkor, ezt úgy tudom elképzelni, Tanító bácsi, hogy a rangsorban elöl álló szám száz százalékos lesz, az utolsó pedig nulla százalékos? Pontosan. Ahogy mondod Pistike! Nézzünk egy példát!

Tehát van öt számunk. Rangsoruk pozícióik az 1, 2, 3, 4 és az 5. Képzeljünk el egy szakaszt, amelynek végpontjai az 1 és az 5, azaz 100% és 0%. Ha azonos távolságra el akarjuk helyezni rajta a többi számot is (2,3 és 4), akkor a szakaszt négy egyenlő részre kell osztani (5 - 1). És a 100%-ot is. Ami 25% lesz.

Általánosítva elmondhatjuk, hogy az egymást követő rangsor-pozíciók közötti százalékos különbség a száz és a sorszámok eggyel csökkentett darabszámának hányadosa, azaz: 100/(<sorszámok>-1).

A rangsor-pozíció százalékosításának ezt a módszerét alkalmazza a SZÁZALÉKRANG.TARTALMAZ függvény is. Funkciója: egy számhalmaz egy eleme rangsor-pozíciójának százalékos értékének megállapítása. Első argumentumával a számokat tartalmazó tartományt, a másodikkal a vizsgált számot kell deklarálnunk.
A függvény három tizedesjegy pontossággal számol. Ez egy tizedesjegyet jelent százalékos megjelenítésben. Például, ha a függvény eredménye 0,745, akkor az százalékos megjelenítésben 74,5%. Ha ez a pontosság nem megfelelő, akkor a harmadik nem kötelező argumentummal határozhatjuk meg, hány tizedesjegy legyen az eredményben. Például, ha a harmadik argumentum 4, akkor a függvény eredménye 0,7457 lesz, ami százalékos megjelenítésben 74,57%-t eredményez. A függvény a pontosságot nem kerekítéssel, hanem csonkolással „állítja be”.
A SZÁZALÉKRANG.KIZÁR függvény is százalékosan állapítja meg a rangsor pozíciót, de a száz- és a nulla százalékot a halmaz egyik elemének sem „osztja ki”. Másként fogalmazva, a SZÁZALÉKRANG.KIZÁR függvény eredménye sohasem lesz egy (1) vagy nulla (0). De hogyan teszi ezt?
A függvény a rangsor-pozíciók százalékosítása előtt két virtuális pozíciót képez, egyet a rangsor elején és egyet a rangsor végén. Tehát lesz egy nulladik és egy n + 1 (elemszám plusz egy) sorszámunk is. Példánknál maradva, az öt elemű halmaz rangsora, a segéd-pozíciókkal együtt, hét sorszámot tartalmaz. Képzeljük el újra a szakaszt, amelynek végpontjai a nulla és az n+1 sorszámok. Ha egyenletesen akarom elhelyezni a további számokat (1, 2, 3, 4 és 5) a szakaszon, akkor a szakasz hosszát hattal kell osztanom. És a száz százalékot is. Ami, három tizedesjegyre csonkolva, 16,6%. Általánosítva, az egymást követő elemek százalékos rangsor-pozíciójának különbsége: 100/(n+1). A rangsorban elől álló elem értéke: 100-100/(n+1).

A két függvény argumentum-listája azonos. A rangsor-pozíciókat a RANG.EGY függvénnyel azonos módon állapítják meg. Ebből következően a halmaz ismétlődő elemeinek, nem csak a rangsor-pozíciója, hanem a pozíció százalékos megfelelője is azonos lesz.
A képlet kiértékelésekor a program az elavult és újabb változatokkal kiváltott függvényeket is feldolgozza. De hogy miért szerepelteti őket a névkiegészítőben, arra nem tudok magyarázatot. Minden esetre, ezeket a pici, felkiáltójeles táblácskával megjelölt függvényeket ne használjuk!
A százalékos rangsor-pozíció nem csak a vizsgált számról, de a halmaz többi eleméről is ad információt. Lássunk egy példát! Van egy számunk 375, ennek a számnak a százalékos rangsor-pozíciója 82,3%. Ez az érték nem csak azt mutatja, hogy a 375, az őt tartalmazó halmaz rangsorának első, „legfelső” ötödébe esik, de azt is, hogy a halmaz elemeinek 82,3% kisebb vagy egyenlő mint 375.
Ha ebből a szemszögből vizsgáljuk a három függvényt, akkor érthetővé válik az a közös tulajdonságuk, hogy nem csak a halmaz elemeinek, hanem a halmaz értéktartományában álló tetszőleges számnak is meg tudják határozni a százalékos „rangsor-pozícióját”. Azért használok idézőjelet, mert a halmazban nem szereplő szám, nem lehet a halmaz rangsorának része, tehát rangsor-pozíciója sincs. A nem létező elem százalékos rangsor-pozícióját a függvények interpolációval képzik. Mondja a Microsoft…
De fordítva is feltehetjük a kérdést, melyik az szám, amelynél a halmaz meghatározott százalékú eleme kisebb vagy egyenlő. A kérdésre a kétargumentumos percentilis függvények adnak választ. Első argumentumukkal a számokat tartalmazó tartományt, a másodikkal a százalékos rangsor-pozíciót kell megadnunk. A második argumentum tizedestörtként és százalékosan is megadható.
A százalékrang és a percentilis függvények tehát ellentétes műveletet végeznek. Ha lekérdezzük egy szám százalékos rangsor-pozícióját, majd az eredményül kapott százalékkal percentilist számítunk, akkor az eredti számhoz jutunk vissza. Természetesen a társ-függvényeket alkalmazva: vagy tartalmaz-tartalmaz vagy kizár-kizár.
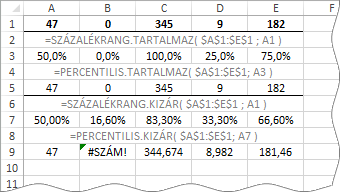
Ahogy a képen látszik a PERCENTILIS.KIZÁR függvény nem áll a helyzet magaslatán. Nem az eredetitől eltérő eredményekre gondolok (345 » 344,679 - 9 » 8,982…), mert azt a számítások eltérő pontossága illetve pontatlansága eredményezi, hanem a B9-es cella hibaértékére. A Microsoft erről ezt mondja: „Ha k (a súgó „k” nak nevezi a második argumentumban megadott százalékos rangsor-pozíciót) értéke adott, és így a függvény nem tudja a percentilis interpolációval meghatározott értékét venni, az Excel a #SZÁM! hibaértékkel tér vissza”. Ez baromira értelmetlen, Tanító bácsi! Az, Pistike!
Az ebben a szövegben bemutatott függvények egy halmaz elemeinek rangsor szerinti felosztásában nyújtanak segítséget. Ez a művelet az élet más területein is használatos. A halmaz elemeinek azonos darabszámú csoportjait kvantiliseknek nevezik. A leggyakoribb kvantilisek a tercilis (a halmaz elemeinek harmada), a kvartilis (a halmaz elemeinek negyede), kvintilis (… ötöde), decilis (… tizede) és a percentilis (… század része).
A kvartiliseket a program függvényeivel képezhetjük. Két kötelező argumentumukkal a szám-halmazt tartalmazó tartományt és a kívánt kvartilis sorszámát kell megadnunk. Utóbbi a KVARTILIS.TARTALMAZ és a KVARTILIS esetében: 4 (100%), 3 (75%), 2 (50%), 1 (25%) és 0 (0%). A KVARTILIS.KIZÁR esetében: 3 (75%), 2 (50%) és 1 (25%)
Van még egy fogalom, amiről beszélni kell. Ha egy tudományos szövegben például az áll, hogy a halmaz legfelső decilise, akkor ez a rangsor elején álló „csoportot”, tehát az első decilist jelenti!

 margitfalvi.arpad@gmail.com
margitfalvi.arpad@gmail.com
