2024-03-18 Excel 2021
kereső függvények
A kereső függvényekkel egy adatpár ismeretlen elemét határozhatjuk meg. A meghatározás az ismert elem pozíciója illetve értéke alapján történik.
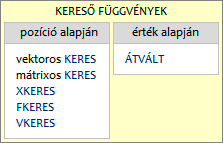
Először beszéljünk a pozíció alapján keresőkről. Ezek a függvények tartományban és tömbben is tudnak dolgozni, ezért a leírásukban, a mindkét objektum szerkezetére jellemző vektor (egy oszlop vagy egy sor) és a mátrix (több sor és több oszlop) fogalmakat fogom használni.
A függvények eredménye az ismeretlen elemet tartalmazó objektum, az ismert elem pozíciójával azonos pozíciójú eleme lesz. Magyarul, ha az ismert elem harmadik a saját objektumában, akkor a függvény eredménye az ismeretlen elemet tartalmazó objektum harmadik eleme lesz. A függvények az ismert elem pozícióját kereséssel állapítják meg. Ebből ered a függvények neve.
Mielőtt továbblépnénk tekintsük át az öt függvény munkaterületét. Persze ez csak idézőjeles munkaterület!
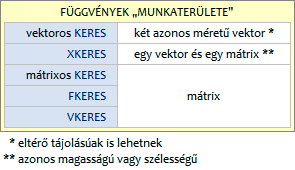
A fenti táblázatból kiderül, hogy a KERES függvénynek van vektoros és van mátrixos változata is. A függvények munkaterületének meghatározott részeiben történik a keresés illetve az eredmény kiválasztása.
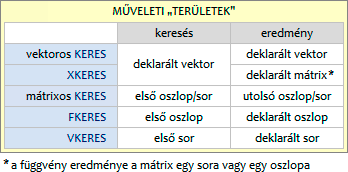
A mátrixos KERES függvény műveleti területeit a mátrix tájolása határozza meg. Ha a mátrixban a sorok száma nagyobb vagy egyenlő az oszlopok számánál, akkor a mátrix álló tájolású, ha az oszlopok száma nagyobb, mint a sorok száma, akkor pedig fekvő. Álló mátrixban a műveleti területek oszlopok, fekvőben pedig sorok.
A fenti táblázat azt mutatja, hogy a függvények mindegyike egy vektorban keresi az ismert elemet. Tehát az ismert elem pozíciója egy sorszám. A sorszámozás balról jobbra és felülről lefelé halad. De nem csak a keresés, hanem az eredmény kiválasztása is vektorból történik. A függvények által visszaadott adat, az eredmény-vektor a kereséssel megállapított számmal azonos sorszámú eleme. Egy kivétellel: az XKERES eredmény-területe egy mátrix. És az eredménye nem egyetlen adat, hanem az eredmény-mátrix az ismert elem sorszámával azonos sorszámú sora illetve oszlopa.
A függvények tehát az első lépésben kereséssel meghatározzák az ismert elem pozícióját. A művelet irányulhat az elem-, vagy az elem kategóriájának megkeresésére. Az ismert elem keresésekor csak a teljes azonosság minősül találatnak, kategorizálás esetében azonban már két eljárás is szóba jöhet. (1) Melyik az a legnagyobb elem a vektorban, amelyik kisebb vagy egyenlő a keresett elemnél. (2) Melyik az a legkisebb elem a vektorban, amely nagyobb vagy egyenlő az ismert elemnél. Az első eljárást „alulról közelítés”-nek, a másodikat „felülről közelítés”-nek nevezzük.
Az XKERES függvény kivételével, csak a teljes egyezéses keresésre illetve az alulról közelítéses kategorizálásra alkalmasak ezek a függvények. És az alulról közelítéses kategorizálást is csak emelkedő rendezettségű vektorban! A tárgyalt függvények közül a legfiatalabb az XKRES. Csak a program legújabb verzióiban (2021, 365) érhető el. Ezzel a függvénnyel mind a három módszerrel kerestethetünk! Sőt még rendeznünk se kell! (Sőt-sőt, még helyettesítő karaktereket is használhatunk szövegek keresésekor.)

Az ÁTVÁLT függvény neve félrevezető, mert nem vált át semmit semmire, hanem mint egy igazi kereső függvény egy adatpár ismeretlen elemét adja eredményül. De nem az ismert elem pozíciója, hanem annak értéke alapján választja ki az eredményt.
Első argumentuma az adatpár ismert eleme. Ezt fogja a függvény keresni: nincs kategorizálás, csak egyenlőség van. Egy kis kibúvóval: szöveg keresésénél a kis- és a nagybetűk nincsenek megkülönböztetve. A további argumentumok párban állnak: adat-eredmény. Az utolsó argumentummal a találat nélküli keresés esetén visszaadandó adatot deklarálhatjuk. Ha akarjuk.

Ugye, nem nehéz az ábrába belelátni a keresési- és az eredmény-vektort? Az ÁTVÁLT függvény argumentumai lehetnek: kifejezések, hivatkozások és tetszőleges adattípusú konstansok.
elágazás-kezelő függvények
A programozók „elágazás”-nak nevezik a program azon pontját, ahol a számítógép alternatív műveletek közül automatikusan választja ki a következő műveletet. A kiválasztás egy vagy több feltétel kiértékelésének eredménye alapján történik.
A táblázatkezelésben is gyakran találkozunk ilyen helyzettel. Egy meghatározott adat feldolgozása csak eltérő műveletekkel lehetséges, mert előfordulásai egy vagy több tulajdonságukban eltérnek. Miről van szó? Például, prémiumról. A félmillió alatti fizetésűek négyszáz-ezret, az a fölöttiek kettőszáz-ezer forintot kapnak.
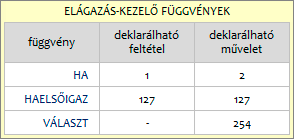
A HA függvény „versikéje” egyszerű. Mi történjen, ha a feltétel teljesül és mi történjen ha nem? Ennek megfelelően deklarálnunk kell a feltételt (első argumentum), az IGAZ-műveletet (második argumentum) és a HAMIS-műveletet (harmadik argumentum).
A HAELSŐIGAZ függvény argumentumaival pedig ezt mondjuk. Itt van ez a csomó feltétel! Mindegyikhez rendeltem egy műveletet. Értékeld ki az első feltételt! Ha a feltétel teljesült, akkor végezd el a hozzárendelt műveletet és utána állj le! Ha nem, akkor folytasd a következő feltétel kiértékelésével! Ha a feltétel teljesült, akkor végezd el a hozzárendelet műveletet és utána állj le! Ha nem… Ennek megfelelően feltétel-művelet párokat kell a függvény argumentumaival deklarálnunk. Legfeljebb százhuszonhetet. Szerintem ennyi elég lesz.
A VÁLASZT függvény esetében nem feltételeket deklarálunk, hanem egy indexelt műveletlistát. A sorszámokat nem mi adjuk, hanem a függvény osztja ki a deklarációk sorrendjében. A sorszám egyessel kezdődik. A VÁLASZT azt a sorszámú műveletet fogja végrehajtani, amelyet az első argumentumával meghatározott kifejezés eredményül ad. Tehát, ezt a függvényt csak akkor tudjuk használni, ha a feldolgozandó adatból vagy annak valamelyik kapcsolódó adatából sorszámot tudunk képezni.
Felmerülhet a kérdés, a HAELSŐIGAZ és a VÁLASZT függvények miért nem biztosítanak „menekülő útvonalat”, ha egyik feltétel sem teljesül vagy nem létező indexet kapunk. Valóban, nincs ilyen argumentumuk, de a HAELSŐIGAZ esetében deklarálhatunk egy biztosan teljesülő feltételt: egy egyenlő eggyel, a VÁLASZT esetében pedig az indexet szolgáltató kifejezést egy HA függvénybe ágyazhatjuk.
véletlenszámot adó függvények
A véletlenszám a „véletlenszerűen kiválasztott szám” rövidítése. A kiválasztás intervallumát az alkalmazott függvény illetve a felhasználó határozza meg. Három függvénnyel kérhetünk véletlenszerűen kiválasztott számot.
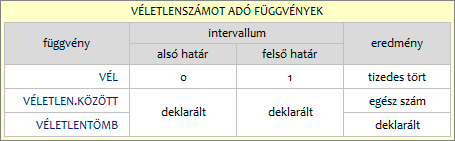
A VÉL és a VÉLETLEN.KÖZÖTT egyetlen számot ad eredményül, a VÉLETLENTÖMB egy a felhasználó által megadott felépítésű tömböt, amelynek elemei a véletlenszerűen kiválasztott számok. A VÉL eredménye tizedes tört, a VÉLETLEN.KÖZÖTT-é egész szám, a VÉLETLENTÖMB pedig kívánság szerint ad tizedes törteket vagy egész számokat.
És tessék mondani, a határértékek is beletartoznak a kiválasztható számok halmazába? Igen, a VÉL függvény egyesének (1) kivételével. Apropó határértékek, a VÉLETLEN.KÖZÖTT és a VÉLETLENTÖMB nem működik, ha a felső határérték kisebb, mint az alsó határérték.
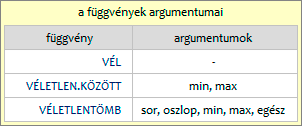
A fenti ábra képleteiben az alsó határértéket „min”-nek, a felsőt „max”-nak neveztem.
A VÉLETLENTÖMB függvénynek van egy vicces tulajdonsága: mindegyik argumentuma elhagyható. Ha nem adjuk meg a sorok számát, akkor a program egynek veszi, ha nem adjuk meg az oszlopok számát, akkor az is egy lesz. Ha hiányzik az alsó határérték, akkor nullával kezdődik a kiválasztható számok intervalluma, ha a felső hiányzik, akkor az egy lesz a legmagasabb kiválasztható szám. És ha az „egész” argumentumot nem adtuk meg, akkor decimális törteket kapunk.

Egy VÉL függvényes képlettel tetszőleges intervallumból kérhetünk véletlenszerűen kiválasztott tizedes törtet vagy egész számot.
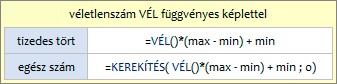
pozíció-meghatározó függvények
Összesen két függvényről van szó, a HOL.VAN-ról és a XHOL.VAN-ról. Vektor a „munkaterülete” mindkettőnek. A vektor lehet tartomány és lehet tömb is. A függvények megállapítják, hogy a keresett adat hányadik a vektorban. A sorszámozás balról jobbra, illetve felülről lefelé halad és egyessel kezdődik. Mindhárom keresés-típusra alkalmasak. A HOL.VAN a keresés típusától függően rendezést igényelhet a vektorban.
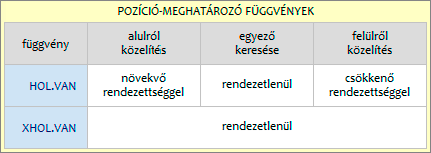
Az XHOL.VAN függvény a HOL.VAN függvény tökéletesítése. De nem csak azért, mert már nem kell a vektort rendezni, hanem a plusz szolgáltatások miatt is: egyező keresésénél megadhatjuk a keresés irányát (a sorszámozás irányát ez nem befolyásolja) és helyettesítő karaktereket is használhatunk. Sőt nagy elemszámú vektor esetén, tetszőleges irányú rendezést követően, kérhetjük a sokkal gyorsabb intervallum-felezéses (bináris keresés) pozíció-meghatározást is. Persze ennek csak több tízezres elemszámú vektor esetén van jelentősége.
képlet-kezelő függvények
Ezt a funkciót is két függvény szolgálja, a KÉPLETSZÖVEG és a LET. Előbbi a képlet-vizsgálat, utóbbi a képlet-szerkesztés eszköze.
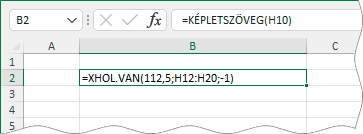
A KÉPLETSZÖVEG függvény az argumentumával meghatározott cella képletét szövegként adja eredményül, beleértve az egyenlőségjelet is.
A LET függvénnyel a képlet műveleteit logikai egységekbe rendezhetjük és ezeket a képletrészeket külön-külön deklarálhatjuk. A képletrészeket, csak a függvény kiértékelésének idejéig érvényes, felhasználói névvel azonosítjuk.
A függvény argumentumai párban állnak: név-képletrész. A program megadásuk sorrendjében dolgozza fel a képletrészeket, majd a részeredményeket a deklarált névvel együtt a memóriában tárolja. Ez a végrehajtási mód teszi lehetővé, hogy a már kiértékelt képletrészek eredményét újabb képletrészek deklarációjában szerepeltethetjük. Másként fogalmazva, a képletrész deklarációja tartalmazhatja, a már deklarált képletrészek nevét. A függvény utolsó argumentuma egy kifejezés, amely a függvény eredményét adja. Vegyünk egy példát, hogy jobban megértsük a fentieket.
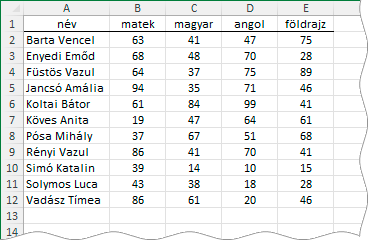
A tanárok nullától száz pontig értékelik a diákok felkészültségét. Kíváncsiak vagyunk a három legjobb angolos pontszámainak átlagára. A képlet szerkesztését egy LET függvénnyel egyszerűsítjük.
A feladat algoritmusa a következő. A SORBA.RENDEZ függvénnyel a táblázat adatsorait tömbösítjük, úgy hogy a legjobb angolosok felül legyenek. Ebből a tömbből az INDEX függvénnyel képezzük az első három legjobb angolos pontszámainak tömbjét. Mivel tömbökkel dolgozunk az INDEX „sorszám” és „oszlopszám” argumentumainak is tömböknek kell lenniük. Ezért létre kell hoznunk a sorok (1-3) és az oszlopok (2-5) indexeinek tömbjét a SORSZÁMLISTA függvénnyel. Miután létrehoztuk a pontszámok tömbjét elvégezhetjük az átlagolást az ÁTLAG függvénnyel.

(REndezettTömb) Az első képletrész a táblázat adatsorainak tömbösítése, az „angol” (4. oszlop) pontszámok szerinti csökkenő (-1) rendezettséggel.
(SorIndexekTömbje) A második képletrész a sor-indexek tömbjének képzése. A tömb háromsoros és egyoszlopos, a számtani sorozat első eleme egy, növekménye szintén egy.
(OszlopIndexekTömbje) A harmadik képletrész az oszlop-indexek tömbjének képzése. A tömb egysoros és négyoszlopos, a számtani sorozat első eleme a kettő, növekménye pedig egy.
(PontSZámok) A negyedik képletrész a pontszámok tömbjének képzése az előzőleg létrehozott három tömb felhasználásával.
Végül átlagoljuk a pontszámok tömbjének elemeit.
konvertálás függvény
Vannak a programnak olyan függvényei is, amelyeket funkciójuk alapján nehéz valamelyik csoportba sorolni. Ilyen a KONVERTÁLÁS függvény is.
A KONVERTÁLÁS függvény mennyiséget alakít át. Egyik mértékegységről a másikra. A cellában álló szám (1) vagy azonosító (2) vagy egy mennyiség mérőszáma. A mennyiség a mérőszámból és a mértékegységből áll. A függvény három argumentuma a mérőszám, a jelenlegi mértékegység és a kívánt mértékegység megadására szolgál.
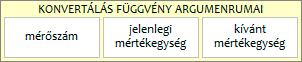
A mértékegységeket a függvény kódjaival kell megadnunk. Beírásukat a névkiegészítő segíti.
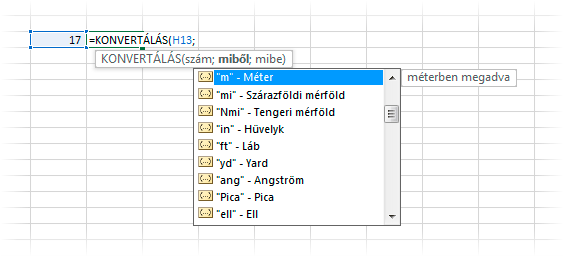
Elképesztő a függvény apparátusa! Tizenhárom tudomány-terület (energia, erő, idő, információ, matematika, mágnesesség, nyomás, sebesség, távolság, teljesítmény, terület, térfogat, tömeg) száztizenhét mértékegységével dolgozhatunk.
És akkor még nem beszéltünk a mértékegységek bináris és decimális hatványairól, amit a függvény leírása (Microsoft ügyfélszolgálat) előtagnak (prefixum) nevez. Például, a tíz harmadik hatványának kódja a ká betű (kilo). A névkiegészítőben nem találunk kilométert csak métert. A métert így kell megadnunk: ”m”. Ha kilométert, akkor azt meg így: ”km”. Azért mesélem ilyen szájbarágósan, mert a függvény leírása félrevezető. Ott a tíz harmadik hatványának kódját így adják meg: ”k”, mintha a kilo-t önállóan kellene deklarálnunk.
A függvény tervezőjének még arra is volt gondja, hogy a harmadik argumentum megadásakor a névkiegészítő listája csak a második argumentumban deklarált mértékegység tudomány-területének mértékegységeit ajánlja fel és nem újra mind a száztizenhetet.
index függvény
A függvény „munkaterülete” egy vagy több tartomány illetve tömb. Az INDEX képlet-környezetének függvényében területe meghatározott elemének tartalmát vagy annak hivatkozását adja eredményül. A függvénynek van egyterületes és van többterületes változata.

Ahogy látjuk a területeket (azonos „méretűek”!) zárójelek között pontosvesszővel kell megadnunk. Sorszámuk (indexük) azonos a deklarációjuk sorszámával.
Az INDEX függvény nem csak egyetlen cella, hanem teljes sor, vagy teljes oszlop, sőt akár teljes terület tartalmát illetve hivatkozását képes visszaadni. Ezt a működést nullás index-szel tudjuk kiváltani.

A függvény definíciójában szereplő, az eredmény típusára vonatkozó, talányos kitétel (képlet-környezet függvényében) magyarázatra szorul. A függvény látszólag az argumentumaival meghatározott objektum tartalmát adja eredményül, de valójában nem azt. Hanem a hivatkozását. Oké, de akkor, hogy lesz mondjuk a D5-ből 328? Egyszerűen. Ha beírjuk egy cellába, hogy =D5, akkor 328-at kapunk eredményül, mert a D5-ben a 328-as szám áll.
Tehát, a függvény eredményét közvetlenül felhasználhatjuk mint hivatkozást. Magyarul, nem kell hozzá az INDIREKT függvény. Mutatok egy példát. A vezetőség összeállította a vállalat éves bevételi tervét, hónapokra lebontva. Minden hónap elején beírjuk a kis táblázatba az előző hónap tényleges bevételét.
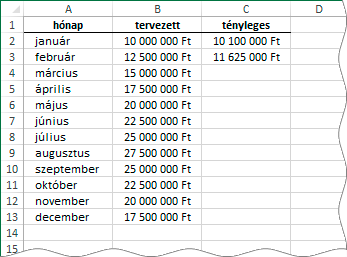
Ha ellenőrizni akarjuk az éves terv végrehajtásának állapotát, akkor a tényleges bevételek összegét el kell osztanunk az ezekre a hónapokra tervezett bevételek összegével. Hogy másolható képletet tudjunk szerkeszteni nevet kell létrehoznunk (terv) az osztás művelet osztójának. Ez egy havonta növekvő tartomány, amelynek első cellája a B2, utolsó cellája pedig az előző hónapra előírt bevétel cellája. Most, azaz 2024 márciusában vizsgáljuk az adatokat.
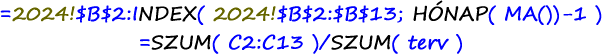
A felső képlet a „terv” név deklarációja az INDEX függvénnyel, alul pedig a tervteljesítés állapotát meghatározó képlet.
kimutatásadatot.vesz függvény
Pivot táblával létrehozott statisztikai értéket a KIMUTATÁSADATOT.VESZ függvénnyel tudjuk a képletben szerepeltetni. Azért kell függvényt használnunk az érték „linkeléséhez”, mert az egyszerű hivatkozás nem követi az elemző-tábla szerkezetének változásait. A függvény és argumentumainak bevitele automatikusan történik a képletbe: nekünk csak rá kell kattintanunk a linkelni szándékozott cellára.
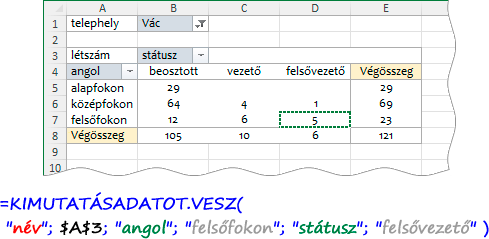
Vegyük sorra a képen látható argumentumokat! Balról jobbra haladva: (1) statisztikai mező neve, (2) a pivot tábla pozíciója, (3) sormező neve, (4) sormező tételének neve, (5) oszlopmező mező neve, (6) oszlopmező tételének neve. És a szűrő mező (telephely) és annak tétele (Vác) hol marad? Hááát... Ők lemaradtak. De, azért nem kell megijedni! A szűrő mező módosítását követően nem csak a pivot táblában, de a képletben is módosul a linkelt statisztikai érték.
Szabadság, egyenlőség, testvériség!

 margitfalvi.arpad@gmail.com
margitfalvi.arpad@gmail.com
